Ford-Fulkerson 方法——最大流问题
最大流&&最小费用最大流&&最大二分匹配
中文是2017年8月的笔记,英文是2018.11月的笔记
英文笔记来自于MIT公开课的笔记,教材为Introduction to Algorithm(Third Edition),根据四位作者姓名首字母大写常称作CLRS,以下是一些资源:
- MIT OCW COURSE HOME
- MIT OCW video
- ppt download links are just under the video frame
- khan academy (brief and easy)
- book: Introduction to Algorithms ( known as CLRS)
- official exercises solution to CLRS
- inofficial exercises solution to CLRS(github)
- inofficial solution(easy to read)
最大流问题
比喻:有一个自来水管道运输系统,起点是 s,终点是 t,途中经过的管道都有一个最大的容量,可以想象每条管道不能被水流“撑爆”。求从 s 到 t 的最大水流量是多少?
应用:网络最大流问题是网络的另一个基本问题。许多系统包含了流量问题。例如交通系统有车流量,金融系统有现金流,控制系统有信息流等。许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。
流网络(Flow Networks):指的是一个有向图 G = (V, E),其中每条边 (u, v) ∈ E 均有一非负容量 c(u, v) ≥ 0。如果 (u, v) ∉ E 则可以规定 c(u, v) = 0。流网络中有两个特殊的顶点:源点 s (source)和汇点 t(sink)。为方便起见,假定每个顶点均处于从源点到汇点的某条路径上,就是说,对每个顶点 v ∈ E,存在一条路径 s –> v –> t。
容量限制(Capacity constraint):对于所有的结点 u, v ∈ V,要求 0 ≤ f(u, v) ≤ c(u, v)
流量限制/流量守恒(Flow conservation):对于所有的结点 u ∈ V - {s, t},要求 Σf(v, u) = Σf(u, v)
We call this property “flow conservation”, and it is equivalent to Kirchhoff’s current law when the material is electrical current.
Flow in equals flow out.
当(u, v) ∉ E时,从结点 u 到结点 v 之间没有流,因此f(u, v) = 0。我们称非负数值f(u, v)为从结点 u 到结点 v 的流,定义如下: |f| = Σf(s, v) - Σf(v, s),也就是说,流 f 的值是从源结点流出的总流量减去流入源结点的总流量。(有点类似电路中的基尔霍夫定律)
Here, the |*|notation denotes flow value, not absolute value or cardinality.
具有多个源结点和多个汇点的网络
- 一个最大流问题可能会包含几个源结点和几个汇点,比如{s1, s2, …, sm} 以及 {t1, t2, …, tm},而不仅仅只有一个源结点和汇点,其解决方法并不比普通的最大流问题难。
- 加入一个超级源结点 s,并对于多个源结点,加入有向边 (s, si) 和容量 c(s, si) = ∞,同时创建一个超级汇点 t,并对于多个汇点,加入有向边 (ti, t) 和容量 c(ti, t) = ∞。
- 这样单源结点能够给原来的多个源结点 si 提供所需要的流量,而单汇点 t 则可以消费原来所有汇点 ti 所消费的流量。
Ford-Fulkerson 方法
We call it a “method” rather than an “algorithm” because it encompasses
several implementations with differing running times.
几个重要的概念
残留网络(residual capacity):容量网络 - 流量网络 = 残留网络
具体说来,就是假定一个网络 G =(V,E),其源点 s,汇点 t。设 f 为 G 中的一个流,对应顶点 u 到顶点 v 的流。在不超过 C(u,v)的条件下(C 代表边容量),从 u 到 v 之间可以压入的额外网络流量,就是边(u,v)的残余容量(residual capacity)。
残余网络 Gf 还可能包含 G 中不存在的边,算法对流量进行操作的目的是增加总流量,为此,算法可能对特定边上的流量进行缩减。为了表示对一个正流量 f(u ,v) 的缩减,我们将边 (u, v) 加入到 Gf中,并将其残余容量设置为 cf(v, u) = f(u ,v)。也就是说,一条边所能允许的反向流量最多能将其正向流量抵消。
残存网络中的这些反向边允许算法将已经发送出来的流量发送回去。而将流量从同一边发送回去等同于缩减该边的流量,这种操作在很多算法中都是必需的。
增广路径(augmenting path): 这是一条不超过各边容量的从 s 到 t 的简单路径,向这个路径注入流量,可以增加整个网络的流量。我们称在一条增广路径上能够为每条边增加的流量的最大值为路径的残余容量,cf(p) = min{cf(u,v) : (u,v)∈路径p}
割:用来证明 “当残留网络中找不到增广路径时,即找到最大流”,最大流最小切割定理,具体证明略。
算法过程:
开始,对于所有结点 u, v ∈ V, f(u, v) = 0,给出的初始流值为0。
在每一次迭代中,将 G 的流值增加,方法就是在残留网络 Gf 中寻找一条增广路径(一般用 BFS 算法遍历残留网络中各个结点,以此寻找增广路径),然后在增广路径中的每条边都增加等量的流值,这个流值的大小就是增广路径上的最大残余流量。
虽然 Ford-Fulkerson 方法每次迭代都增加流值,但是对于某条特定边来说,其流量可能增加,也可能减小,这是必要的,详情见下文的“反向边”。
重复这一过程,直到残余网络中不再存在增广路径为止。最大流最小切割定理将说明在算法终结时,该算法获得一个最大流。
伪代码:
FORD-FULKERSON(G,t,s) 1 for each edge(u,v) 属于 E(G) 2 do f[u,v]=0 3 f[v,u]=0 4 while there exists a path p from s to t in the residual network Gf // 根据最大流最小切割定理,当不再有增广路径时,流 f 就是最大流 5 do cf(p)=min{cf(u,v):(u,v)is in p} // cf(p)为该路径的残余容量 6 for each edge (u,v) in p 7 do f[u,v]=f[u,v]+cf(p) //为该路径中的每条边中注入刚才找到到的残余容量 8 f[v,u]=-f[u,v] //反向边注入反向流量反向边是什么?
假设没有上面伪代码中最后一步的操作,那么对于如下的流网络:
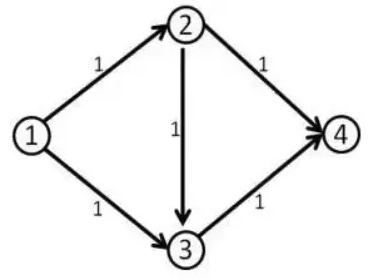
我们第一次找到了 1-2-3-4 这条增广路,这条路上的最小边剩余流量显然是 1。于是我们修改后得到了下面这个残留网络:
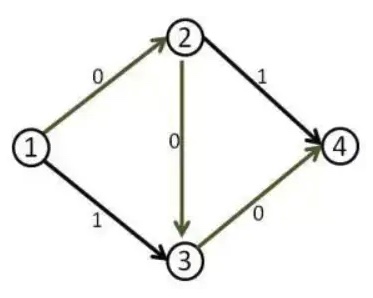
这时候 (1,2) 和 (3,4) 边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是 1。但这个答案明显不是最大流,因为我们可以同时走 1-2-4 和 1-3-4,这样可以得到流量为 2 的流。
这是贪婪算法行不通的一个例子(摘自《算法与数据结构 C++语言描述》第四版,但翻译很差劲,推荐读原版)
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边 (i,j) 都有一条反向边 (j,i),反向边也同样有它的容量。那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个后悔的机会,应该有一个不走 (2-3-4) 而改走 (2-4) 的机制。
我们来看刚才的例子,在找到 1-2-3-4 这条增广路之后,把容量修改成如下:
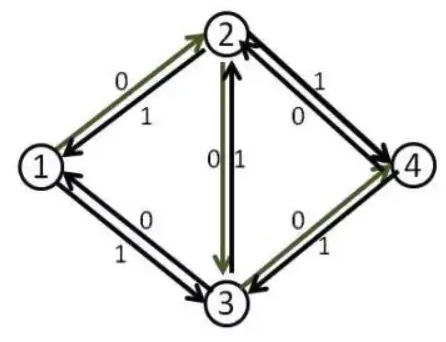
这时再找增广路的时候,就会找到 1-3-2-4 这条可增广量,即 delta 值为 1 的可增广路。将这条路增广之后,得到了最大流 2。
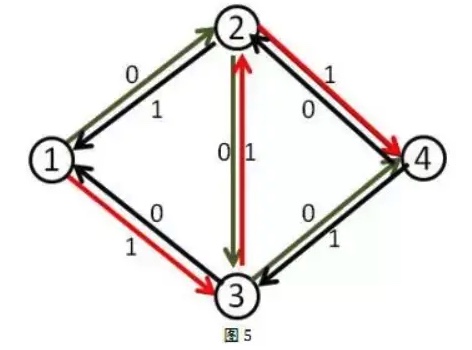
解释:
事实上,当我们第二次的增广路走 3-2 这条反向边的时候,就相当于把 2-3 这条正向边已经是用了的流量给” 退” 了回去,不走 2-3 这条路,而改走从 2 点出发的其他的路也就是 2-4。(有人问如果这里没有 2-4 怎么办,这时假如没有 2-4 这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在 3-4 上的流量由 1-3-4 这条路来” 接管”。而最终 2-3 这条路正向流量 1,反向流量 1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会。
The intuition behind this definition(反向边) follows the definition of the residual network.
We increase the flow on (u, v) by f’(u, v) but decrease it by f’(u, v) because pushing flow on the reverse edge in the residual network signifies decreasing the flow in the original network.Pushing flow on the reverse edge in the residual network is also known as cancellation.
关于反向边的讨论——Modeling problems with antiparallel edges
Our original assumption: if an edge (v1, v2) ∈ E, then (v2, v1) ∉ E.
What if we violate this assumption? Thus, we have (v2, v1) ∈ E. We call the two edges (v1, v2) and (v2, v1) antiparallel.
How to solve this problem? We could convert a graph with antiparallel edges into a graph wihout antiparallel edges:
- Split (v1, v2) by adding a new vertex v’ and replacing edge (v1, v2) with the pair of edge (v1, v’) and (v’, v2).
- Set the capacity of both new edges to the capacity of the original edge.
- Thus, the resulting network satisfies the property that if an edge is in the network, the reverse is not.
总之,antiparallel是允许存在的,引入一个新节点即可把带antiparallel的图转换为不带antiparallel的图
最大流-最小割定理
最大流-最小割定理用来证明Ford-Fulkson方法的确达到了最大流
Cuts of flow networks
The Ford-Fulkerson method repeatedly augments the flow along augmenting paths until it has found a maximum flow.
How do we know that when the algorithm terminates, we have actually found a maximum flow?
The max-flow min-cut theorem, which we shall prove shortly, tells us that a flow is maximum if and only if its residual network contains no augmenting path.
To prove this theorem, though, we must first explore the notion of a cut of a flow network.
You can overview cut theory in my preview note of minimum spanning tree.
Definition:
If f is a flow, then the net flow f(S, T) across the cut (S, T) is defined to be
f(S, T) = Σu∈SΣv∈T f(u, v) - Σu∈SΣv∈T f(v, u)
The capacity of the cut (S, T) is
c(S, T) = Σu∈SΣv∈T c(u, v)
A minimum cut of a network is a cut whose capacity is minimum over all cuts of the network.
Let f be a flow in a flow network G with source s and sink t, and let (S, T) be any cut of G. Then the net flow across (S, T) is
f(S, T) = |f|
The value of any flow f in a flow network G is bounded from above by the capacity of any cut of G
Theorem 26.6 (Max-flow min-cut theorem)
If f is a flow in a flow network G(V, E) with source s and sink t, then the
following conditions are equivalent:- f is a maximum flow in G.
- The residual network Gf contains no augmenting paths.
- |f| = c(S, T) for some cut (S, T) of G.
算法的效率及其优化—— Edmonds-Karp 算法
如果使用广度优先搜索(BFS)来寻找增广路径,那么可以改善 FORD-FULKERSON 算法的效率,也就是说,每次选择的增广路径是一条从 s 到 t 的最短路径,其中每条边的权重为单位距离(即根据边的数量来计算最短路径),我们称如此实现的 FORD-FULKERSON 方法为 Edmonds-Karp 算法。其运行时间为 O(VE^2)。
注意 E-K 算法适用于改善 F-F 算法的效率,边的权重仅仅还是容量限制,而下文的“最小费用最大流”中的每条边的权重有两个值:(容量限制,单位流量损耗)。
最大流实例
对于如下拓扑图,给出从S1到S6允许的流的方向和带宽限制:
求出S1到S6最大可能带宽(提示Ford-Fulkerson算法)。
画出流的流向及带宽分配,使达到最大可能的带宽。
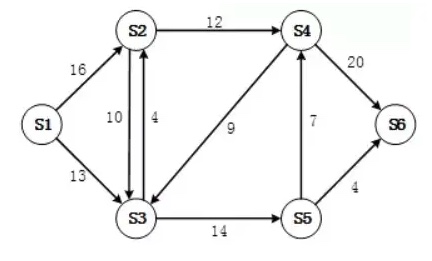
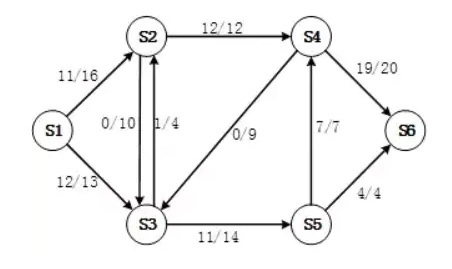
根据算法,最大流的值为23(定值),而下图是一种可能的流量走向:
源码:https://github.com/edisonleolhl/DataStructure-Algorithm/blob/master/Graph/MaxFlow/maxflow.py
在寻找增广路径时用到了 BFS 算法,以后有时间再写写 BFS、DFS 的文章,注意用到了 Python 中的标准库:deque,这是双端队列。
CLRS Exercies
本节摘录了一些算法导论上的对应习题
26.1-5
State the maximum-flow problem as a linear-programming problem.
Solution:
max ∑f(s, v) - ∑f(v,s)
s.t. 0 ≤ f(u, v) ≤ c(u, v)
∑f(v, u) - ∑f(u, v) = 0
26.1-6
Professor Adam has two children who, unfortunately, dislike each other. The problem is so severe that not only do they refuse to walk to school together, but in fact each one refuses to walk on any block that the other child has stepped on that day. The children have no problem with their paths crossing at a corner. Fortunately both the professor’s house and the school are on corners, but beyond that he is not sure if it is going to be possible to send both of his children to the same school. The professor has a map of his town. Show how to formulate the problem of determining whether both his children can go to the same school as a maximum-flow problem.
Solution:
Create a vertex for each corner, and if there is a street between corners u and v, create directed edges (u,v) and (v,u).
Set the capacity of each edge to 1. Let the source be corner on which the professor’s house sits, and let the sink be the corner on which the school is located.
We wish to find a flow of value 22 that also has the property that f(u,v) is an integer for all vertices u and v.
Such a flow represents two edge-disjoint paths from the house to the school.
26.1-7
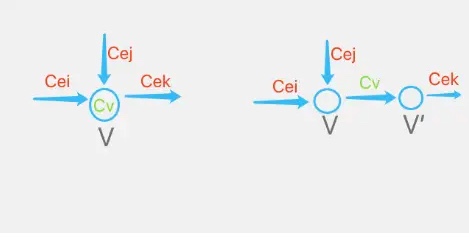
Suppose that, in addition to edge capacities, a flow network has vertex capacities. That is each vertex vv has a limit l(v) on how much flow can pass though vv. Show how to transform a flow network G=(V,E) with vertex capacities into an equivalent flow network G′=(V′,E′) without vertex capacities, such that a maximum flow in G′ has the same value as a maximum flow in G. How many vertices and edges does G′ have?
Solution:
We will construct G′ by splitting each vertex v of G into two vertices v1, v2, joined by an edge of capacity l(v). All incoming edges of vv are now incoming edges to v1. All outgoing edges from vv are now outgoing edges from v2.
More formally, construct G′=(V′,E′) with capacity function c′ as follows. For every v∈V, create two vertices v1, v2 in V′. Add an edge (v1,v2) in E′ with c′(v1,v2)=l(v). For every edge (u,v)∈E, create an edge (u2,v1) in E′ with capacity c′(u2,v1)=c(u,v). Make s1 and t2 as the new source and target vertices in G′. Clearly, |V′|=2|V| and |E′|=|E|+|V|.
I draw a picture to vividly illustrate the idea.
最小费用最大流
最小费用最大流问题是经济学和管理学中的一类典型问题。在一个网络中每段路径都有 “容量” 和 “费用” 两个限制的条件下,此类问题的研究试图寻找出:流量从 A 到 B,如何选择路径、分配经过路径的流量,可以在流量最大的前提下,达到所用的费用最小的要求。如 n 辆卡车要运送物品,从 A 地到 B 地。由于每条路段都有不同的路费要缴纳,每条路能容纳的车的数量有限制,最小费用最大流问题指如何分配卡车的出发路径可以达到费用最低,物品又能全部送到。
注意:最后得到的流必须是最大流,最大流可能有多种情况,目标是找出最小费用的那种情况。
解决最小费用最大流问题,一般有两条途径。
一条途径是先用最大流算法算出最大流,然后根据边费用,检查是否有可能在流量平衡的前提下通过调整边流量,使总费用得以减少?只要有这个可能,就进行这样的调整。调整后,得到一个新的最大流。然后,在这个新流的基础上继续检查,调整。这样迭代下去,直至无调整可能,便得到最小费用最大流。这一思路的特点是保持问题的可行性(始终保持最大流),向最优推进。
另一条解决途径和前面介绍的最大流算法思路相类似,一般首先给出零流作为初始流。这个流的费用为零,当然是最小费用的。然后寻找一条源点至汇点的增流链,但要求这条增流链必须是所有增流链中费用最小的一条。如果能找出增流链,则在增流链上增流,得出新流。将这个流做为初始流看待,继续寻找增流链增流。这样迭代下去,直至找不出增流链,这时的流即为最小费用最大流。这一算法思路的特点是保持解的最优性(每次得到的新流都是费用最小的流),而逐渐向可行解靠近(直至最大流时才是一个可行解)。
第二种办法与前文的 Ford-fulkerson 方法很像,所以选择它更方便,如何找到费用最小的增链流呢?可以用最短路径算法,这里是单源最短路径,所以选择 Dijkstra 算法找出最短路径即可,关于 Dijkstra 的介绍见:http://www.jianshu.com/p/8ba71199a65f,里面有 Python 实现的程序。
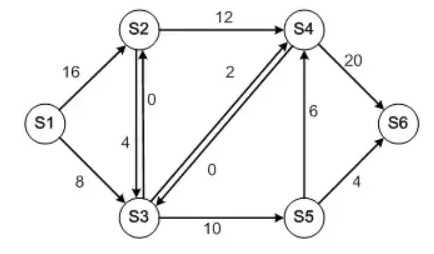
最小费用最大流实例
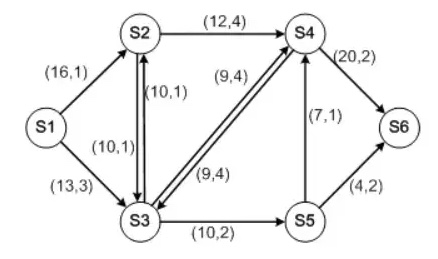
对于如下拓扑图,给出从S1到S6允许的流的方向和带宽限制,链路按带宽收费,以括号形式表示为(带宽容量,单位带宽费用):
求出S1到S6最小费用下最大可能带宽,得出最小费用值,并标出选路状况。
写出对给出任意拓扑图的通用算法描述。
源码:https://github.com/edisonleolhl/DataStructure-Algorithm/blob/master/Graph/MaxFlow/mincostmaxflow.py
运行截图:
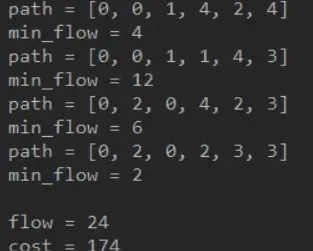
注意增广路径是回溯的,比如第一条增广路径,终点为5,path[5]=4,所以它的前驱是4,path[4]=2,所以4的前驱是2,2的前驱是1,1的前驱是0,所以这条路径是 0-1-2-4-5,也就是 s1-s2-s3-s5-s6。
注意在寻找增广路径时用到了 Dijkstra 算法,至于为什么用 heapq (最小堆的实现),因为它每次 pop 出来的都是最小的项目,根据 Dijkstra ,每次要从未访问点中找到最小距离的顶点,这样就可以巧妙实现。
流量分布情况:
最大二分匹配
最大匹配定义:给定一个无向图 G = (V, E),一个匹配是指:E 的某个子集 M , 对于所有的结点 v ∈ V,子集 M 中最多有一条边与 v 相连,如果子集 M 中的某条边与 v 相连,那么称 v 由 M 匹配;否则 v 就是没有匹配的。最大匹配是指:对于所有任意匹配 M’,有 |M| ≥ |M’| 的匹配 M 。
二分图定义:设 G=(V,E) 是一个无向图,如果顶点 V 可分割为两个互不相交的子集 (A,B),并且图中的每条边(i,j)所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集 (i in A,j in B),则称图 G 为一个二分图。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
应用:把机器集合 L 与任务集合 R 相匹配, E 中有边 (u, v) 就说明一台特定的机器 u ∈ L 能够完成一项特定的任务 v ∈ R,最大二分匹配就是让尽可能多的机器运行起来,因为一台机器只能同时做一个任务,一个任务也只能同时被一个机器完成,所以这里也可理解为让尽可能多的任务被完成。
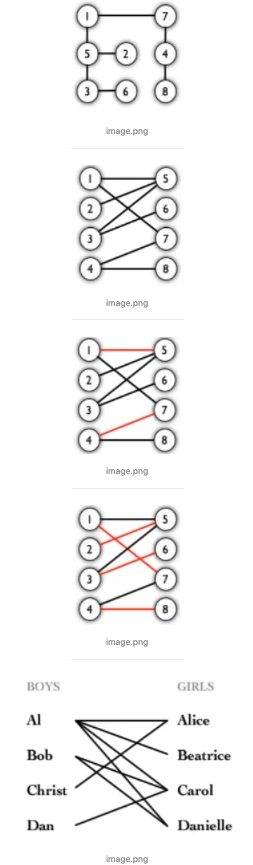
用下图说明,图 1 是二分图,为了直观,一般画成 2 那样,3、4 中红色边即为匹配,4 是最大匹配,同时也是完美匹配(所有顶点都是匹配点),图 5 展示了男孩和女孩暗恋关系,有连线就说明这一对能成,求最大匹配就是求能成多少对
Ford-Fulkson方法解决最大二分匹配
给定如下的二分图(忽略颜色):
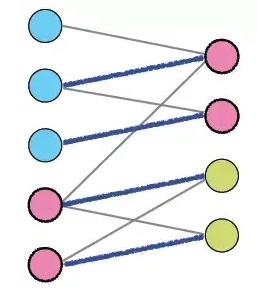
把已有的边设为单向边(方向 L -> R),且各边容量设为 ∞ ;增加源结点 s 与汇点 t,将 s 与集合 L 中各个结点之间构造单向边,且各边容量设为 1;同样的,将集合 R 中各个结点与 t 之间构造单向边,且各边容量设为 1。这时得到一个流网络 G’,如下:
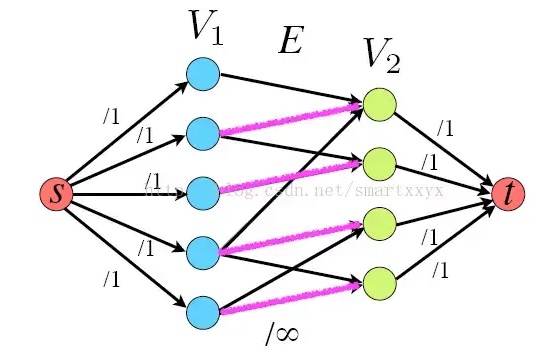
这时,最大匹配数值就等于流网络 G’ 中最大流的值。
匈牙利算法解决二分匹配
推荐文章:趣写算法系列之 – 匈牙利算法
关键就是腾挪,迭代地腾挪
原文发表于 https://www.jianshu.com/p/efb2d79e2b0f, 2017.09.08 12:35:35