遗传算法

前言

  • 之前给小灯神做文本分析的时候，去图书馆借了两本书，一本是《数据之魅：基于开源工具的数据分析》，这本书适合学统计的相关人士学习，现在放在书架上吃灰中，另外一本是《集体智慧编程》，挺有意思的，没有讲很复杂的算法理论，用 Python 把机器学习相关的内容明明白白地、清清楚楚地写清楚了，其中在优化这一章就讲到了遗传算法，与其他章节一样，我也是把源码跑了一下就翻页了。

  • 最近有个同学找我帮忙，应该是课程设计作业之类的，题目如下：

    2017125-deng

  • 要求：

    1. 思考一种算法或规则，求解出灯布局的优化方案。指出算法过程步骤或规则，可以用示意性的代码或流程图表示；
    2. 基于你提出的算法，找到一种新的布局，使得照度均匀度达到最优，请参考上述MATLAB程序作修改并生成三维图形，判断均匀度效果，尝试画出灯的布局图。

  • 这个要求是房间内任何一个点的光照强度尽量平均，越平均越好，光照强度与光源距离成反比。

  • 灯管24个，相当于24个元素共同完成目标，每个元素是二维的（高度固定为3米），有横坐标和纵坐标。

  • 成本函数可以简单用光照强度的方差来评估，某个 solution 的方差越小，那么其成本函数也越小，即越优。

  • 看上去挺简单的，我认为遗传算法是个不错的选择，特别是算法中的变异和交叉操作，每次迭代都能向全局最优解靠近。

算法介绍

  • 想看完整的算法详解去其他博客看就好了，肯定比我写得好，我就偷懒一会，摘抄一些介绍。

百度百科

  • 遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

  • 遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。

  • 染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。

  • 因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

《集体智慧编程》

  • 截图

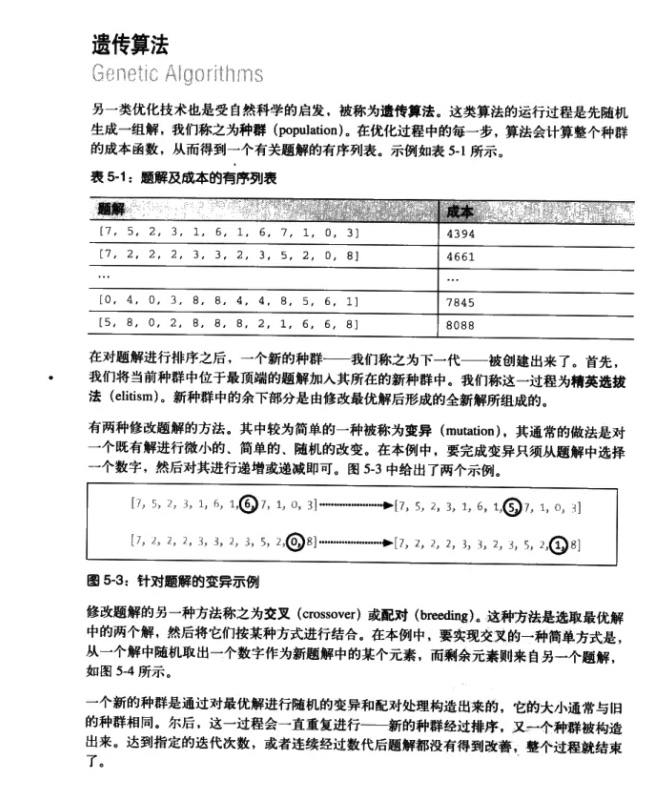
    2017125-ga

    2017125-ga2

    2017125-ga3

  • 书上的源码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    def geneticoptimize(domain, costf, popsize=50, step=1,
                        mutprob=0.2, elite=0.2, maxiter=100):
        # Mutation Operation
        def mutate(vec):
            i = random.randint (0, len (domain) - 1)
            if random.random () < 0.5 and vec[i] > domain[i][0]:
                return vec[0:i] + [vec[i] - step] + vec[i + 1:]
            elif vec[i] < domain[i][1]:
                return vec[0:i] + [vec[i] + step] + vec[i + 1:]

        # Crossover Operation
        def crossover(r1, r2):
            i = random.randint (1, len (domain) - 2)
            return r1[0:i] + r2[i:]

        # Build the initial population
        pop = []
        for i in range (popsize):
            vec = [random.randint (domain[i][0], domain[i][1])
                for i in range (len (domain))]
            pop.append (vec)

        # How many winners from each generation?
        topelite = int (elite * popsize)

        # Main loop
        for i in range (maxiter):
            scores = [(costf (v), v) for v in pop]
            scores.sort ()
            ranked = [v for (s, v) in scores]

            # Start with the pure winners
            pop = ranked[0:topelite]

            # Add mutated and bred forms of the winners
            while len (pop) < popsize:
                if random.random () < mutprob:

                    # Mutation
                    c = random.randint (0, topelite)
                    pop.append (mutate (ranked[c]))
                else:

                    # Crossover
                    c1 = random.randint (0, topelite)
                    c2 = random.randint (0, topelite)
                    pop.append (crossover (ranked[c1], ranked[c2]))

            # Print current best score
            print scores[0][0]

        return scores[0][1]

实践

  • 我并没有直接用 Python 的源码解决问题，学弟的课程应该都是用 Matlab 仿真的，所以我就用忘光了的 Matlab 来练练手。

  • 代码移植的坑就不必说了，移植的过程中我才体会到 Python 是多么的平易近人！！！

  • Life is short, I use Python.

  • 除开代码移植花了挺久时间以外，还有一个很重要的点：源码只解决了一维的问题（一个列表/数组），而灯管问题是二维的，所以有几处地方要修改一下。

    • 首先在初始化种群时，Python 利用列表生成式可以很方便的操作。

      1
      2
      3
      4
      5
      6
      # Build the initial population
      pop = []
      for i in range (popsize):
          vec = [random.randint (domain[i][0], domain[i][1])
              for i in range (len (domain))]
          pop.append (vec)

    • 在 Matlab 中就要麻烦一点，因为是二维的，所以 sol 是 2x24 的矩阵，每列代表一个灯管的坐标，第一行是灯管的y轴坐标（0到12），第二行是灯管的x轴坐标（0到17.5），共有24个灯管，为了代码的可移植性，我用变量 number 表示24。Python 列表的 append 的操作在 Matlab 中可以用 x = [x, y] 代替，但是 Matlab 本质上还是处理矩阵，所以这里的 x y 都是矩阵，以后访问某个序号时还得计算一番，略微麻烦，但没办法，我只想到这个法子。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      pop=[];
      cost=[];
      for i=1:popsize
          sol=unifrnd(0,1,2,number);
          sol(1,:) = sol(1,:).*12;
          sol(2,:) = sol(2,:).*17.5;
          cost = [cost, costf(sol,xx,yy,m,n,number)];
          pop = [pop, sol];
      end

    • Python 中关于种群排序，不得不说列表生成式是真的简单好用。

      1
      2
      3
      scores = [(costf (v), v) for v in pop]
      scores.sort ()
      ranked = [v for (s, v) in scores]

    • Matlab 中关于种群排序，这里我就没有用到 scores 变量了，只有 ranked 才是后面需要的，可以看到，这里在 pop 中访问某个 sol 时挺麻烦的，比如访问第一个 sol，得访问第1列到第24列，所以别忘记把临时变量替换进去，我最开始写代码时就忘了写，导致 Matlab 报错：索引维度不一致。

      1
      2
      3
      4
      5
      [ranked_cost,index_array] = sort(cost); 
      ranked = [];
      for r = 1:length(index_array)
          ranked = [ranked, pop(1:2, (number*(index_array(r)-1)+1):number*index_array(r))];
      end

    • Python 中关于变异（mutate）的函数：

      1
      2
      3
      4
      5
      6
      7
      # Mutation Operation
      def mutate(vec):
          i = random.randint (0, len (domain) - 1)
          if random.random () < 0.5 and vec[i] > domain[i][0]:
              return vec[0:i] + [vec[i] - step] + vec[i + 1:]
          elif vec[i] < domain[i][1]:
              return vec[0:i] + [vec[i] + step] + vec[i + 1:]

    • Matlab 中关于变异（mutate）的函数：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      % vec is a 2-d matrix, number is the length of the solution(number of lights)
      function vec=mutate(vec,number)
          i = floor(rand*(number-1)+0.5)+1;
          flag = rand;
          if flag<0.25 & vec(1,i)>1 & vec(2,i)>1
              vec = [vec(1:2,1:i-1),[vec(1,i)-1,vec(2,i)-1]',vec(1:2,i+1:length(vec))];
          elseif flag<0.5 & vec(1,i)>1 & vec(2,i)<16.5
              vec = [vec(1:2,1:i-1),[vec(1,i)-1,vec(2,i)+1]',vec(1:2,i+1:length(vec))];
          elseif flag<0.75 & vec(1,i)<11 & vec(2,i)>1
              vec = [vec(1:2,1:i-1),[vec(1,i)+1,vec(2,i)-1]',vec(1:2,i+1:length(vec))];
          elseif vec(1,i)<11 & vec(2,i)<16.5
              vec = [vec(1:2,1:i-1),[vec(1,i)+1,vec(2,i)+1]',vec(1:2,i+1:length(vec))];
          else
          end
      end

结果

  • 输出

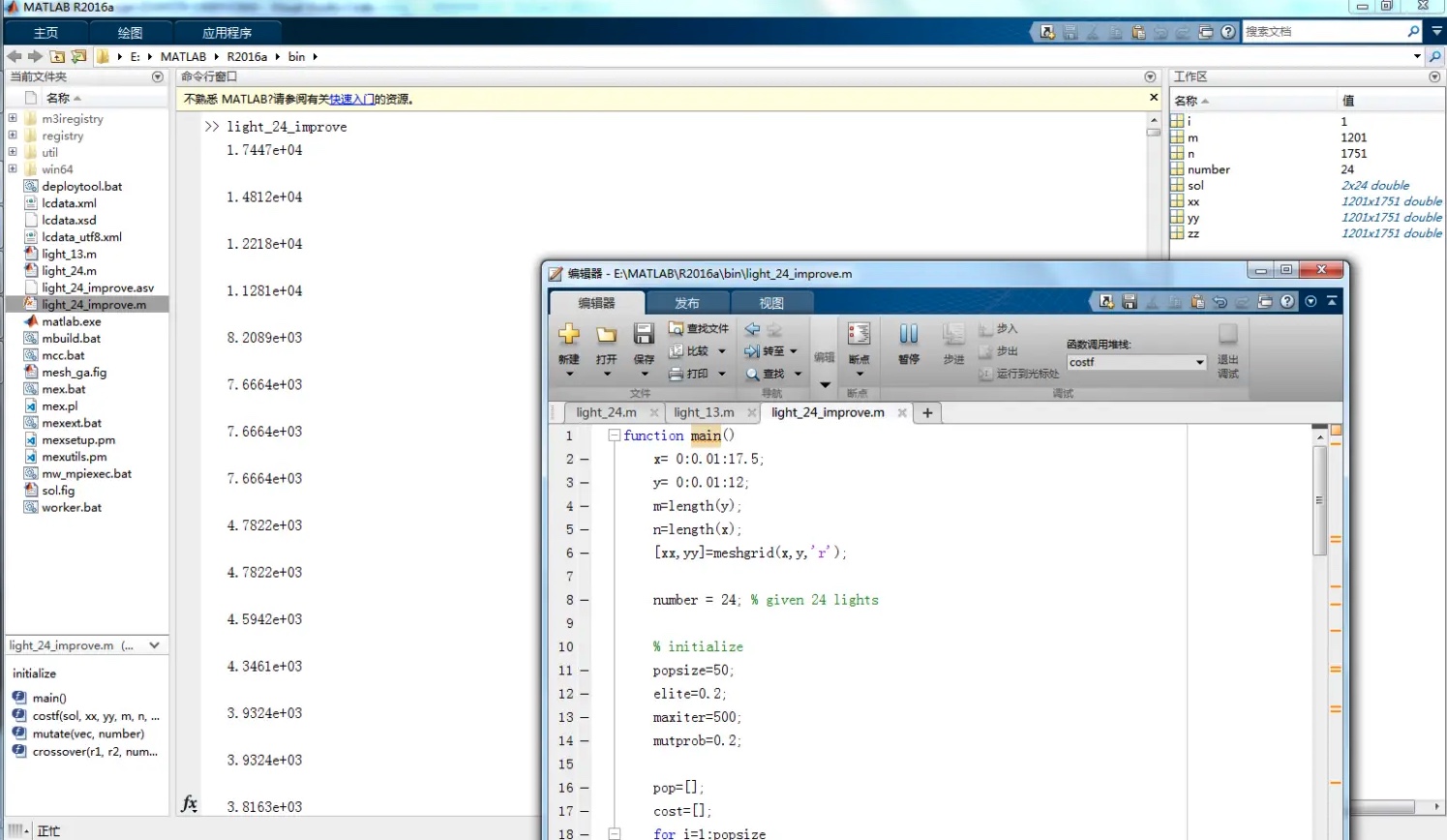
    2017125-result

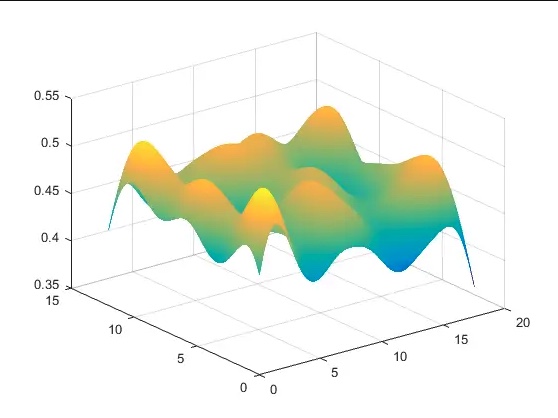
    2017125-mesh

  • 在代码中可以自己设置 maxiter 最大迭代次数，本篇的遗传算法是比较简单的，如果初始化种群比较接近全局最优解的话，那么最后的结果也会非常好看。

Python 源码地址：https://github.com/edisonleolhl/Programming-Collective-Intelligence-Source-Code/blob/master/%E7%AC%AC5%E7%AB%A0%20%E4%BC%98%E5%8C%96/optimization.py

Matlab 源码地址：https://github.com/edisonleolhl/DataStructure-Algorithm/blob/master/Optimization/light_24_improve.m

本文发表于 https://www.jianshu.com/p/7a6f56602f9a, 2017.12.05